[u,v], ...options...)
[dxdt,dydt], ...options...)
[dudt,dvdt], [u,v], ...options...)
Dibuja un campo de direcciones en dos dimensiones x y y.
dydx, dxdt y dydt son expresiones que dependen de x y
y. Además de esas dos variables, las dos expresiones pueden depender de
un conjunto de parámetros, con valores numéricos que son dados por medio
de la opción parameters (la sintaxis de esa opción se explica mas al
frente), o con un rango de posibles valores definidos con la opción
sliders.
Varias otras opciones se pueden incluir dentro del comando, o
seleccionadas en el menú. Haciendo click en un punto del gráfico se
puede hacer que sea dibujada la curva integral que pasa por ese punto;
lo mismo puede ser hecho dando las coordenadas del punto con la opción
trajectory_at dentro del comando plotdf. La dirección de
integración se puede controlar con la opción direction, que
acepta valores de forward, backward ou both. El
número de pasos realizado en la integración numérica se controla
con la opción nsteps y el incremento del tiempo en cada paso
con la opción tstep. Se usa el método de Adams Moulton para
hacer la integración numérica; también es posible cambiar para el
método de Runge-Kutta de cuarto orden con ajuste de pasos.
Menú de la ventana del gráfico:
El menú de la ventana gráfica dispone de las siguientes opciones: Zoom, que permite cambiar el comportamiento del ratón, de manera que hará posible el hacer zoom en la región del gráfico haciendo clic con el botón izquierdo. Cada clic agranda la imagen manteniendo como centro de la misma el punto sobre el cual se ha hecho clic. Manteniendo pulsada la tecla Shift mientras se hace clic, retrocede al tamaño anterior. Para reanudar el cálculo de las trayectorias cuando se hace clic, seleccine la opción Integrate del menú.
La opción Config del menú se puede utilizar para cambiar la(s) EDO(S) y algunos otros ajustes. Después de hacer los cambios, se debe utilizar la opción Replot para activar los nuevos ajustes. Si en el campo Trajectory at del menú de diálogo de Config se introducen un par de coordenadas y luego se pulsa la tecla retorno, se mostrará una nueva curva integral, además de las ya dibujadas. Si se selecciona la opción Replot, sólo se mostrará la última curva integral seleccionada.
Manteniendo pulsado el botón derecho del ratón mientras se mueve el cursor, se puede arrastrar el gráfico horizontal y verticalmente. Otros parámetros, como pueden ser el número de pasos, el valor inicial de t, las coordenadas del centro y el radio, pueden cambiarse en el submenú de la opción Config.
Con la opción Save, se puede obtener una copia del gráfico en una impresora Postscript o guardarlo en un fichero Postscript. Para optar entre la impresión o guardar en fichero, se debe seleccionar Print Options en la ventana de diálogo de Config. Una vez cubiertos los campos de la ventana de diálogo de Save, será necesario seleccionar la opción Save del primer menú para crear el fichero o imprimir el gráfico.
Opciones gráficas:
La función plotdf admite varias opciones, cada una de las cuales
es una lista de dos o más elementos. El primer elemento es el nombre de
la opción, y el resto está formado por el valor o valores asignados
a dicha opción.
La función plotdf reconoce las siguientes opciones:
- tstep establece la amplitud de los incrementos en la variable independiente t, utilizados para calcular la curva integral. Si se aporta sólo una expresión dydx, la variable x será directamente proporcional a t. El valor por defecto es 0.1.
-
nsteps establece el número de pasos de longitud
tstepque se utilizarán en la variable independiente para calcular la curva integral. El valor por defecto es 100. -
direction establece la dirección de la variable
independiente que será seguida para calcular una curva integral.
Valores posibles son:
forward, para hacer que la variable independiente aumentenstepsveces, con incrementoststep;backward, para hacer que la variable independiente disminuya;both, para extender la curva integralnstepspasos hacia adelante ynstepspasos hacia atrás. Las palabrasrightyleftse pueden utilizar como sinónimos deforwardybackward. El valor por defecto esboth. - tinitial establece el valor inicial de la variable t utilizado para calcular curvas integrales. Puesto que las ecuaciones diferenciales son autónomas, esta opción sólo aparecerá en los gráficos de las curvas como funciones de t. El valor por defecto es 0.
-
versus_t se utiliza para crear una segunda ventana
gráfica, con el gráfico de una curva integral, como dos funciones
x, y, de variable independiente t. Si se le da a
versus_tcualquier valor diferente de 0, se mostrará la segunda ventana gráfica, la cual incluye otro menú, similar al de la ventana principal. El valor por defecto es 0. - trajectory_at establece las coordenadas xinitial y yinitial para el extremo inicial de la curva integral. No tiene asignado valor por defecto.
-
parameters establece una lista de parámetros,
junto con sus valores numéricos, que son utilizados en la
definición de la ecuación diferencial. Los nombres de los
parámetros y sus valores deben escribirse en formato de cadena
de caracteres como una secuencia de pares
nombre=valorseparados por comas. -
sliders establece una lista de parámetros que
se cambiarán interactivamente utilizando barras de deslizamiento,
así como los rangos de variación de dichos parámetros.
Los nombres de los parámetros y sus rangos deben escribirse en formato
de cadena de caracteres como una secuencia de pares
nombre=min:maxseparados por comas. - xfun establece una cadena de caracteres con funciones de x separadas por puntos y comas para ser representadas por encima del campo de direcciones. Estas funciones serán interpretadas por Tcl, no por Maxima.
- xradius es la mitad de la longitud del rango de valores a representar en la dirección x. El valor por defecto es 10.
- yradius es la mitad de la longitud del rango de valores a representar en la dirección y. El valor por defecto es 10.
- xcenter es la coordenada x del punto situado en el centro del gráfico. El valor por defecto es 0.
- ycenter es la coordenada y del punto situado en el centro del gráfico. El valor por defecto es 0.
- width establece el ancho de la ventana gráfica en píxeles. El valor por defecto es 500.
- height establece la altura de la ventana gráfica en píxeles. El valor por defecto es 500.
Ejemplos:
NOTA: Dependiendo de la interface que se use para Maxima, las funciones
que usan openmath, incluida plotdf, pueden desencadenar un
fallo si terminan en punto y coma, en vez del símbolo de
dólar. Para evitar problemas, se usará el símbolo de
dólar en todos ejemplos.
-
Para mostrar el campo de direcciones de la ecuación diferencial
y' = exp(-x) + y y la solución que pasa por (2, -0.1):
(%i1) load("plotdf")$ (%i2) plotdf(exp(-x)+y,[trajectory_at,2,-0.1]);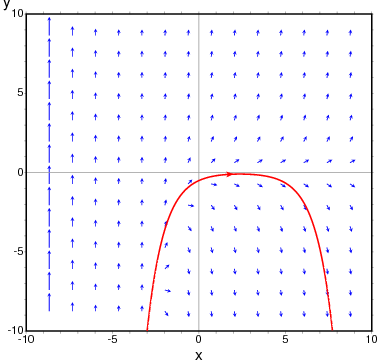
-
Para mostrar el campo de direcciones de la ecuación
diff(y,x) = x - y^2 y la solución de condición
inicial y(-1) = 3, se puede utilizar la sentencia:
(%i3) plotdf(x-y^2,[xfun,"sqrt(x);-sqrt(x)"], [trajectory_at,-1,3], [direction,forward], [yradius,5],[xcenter,6]);El gráfico también muestra la función y = sqrt(x).
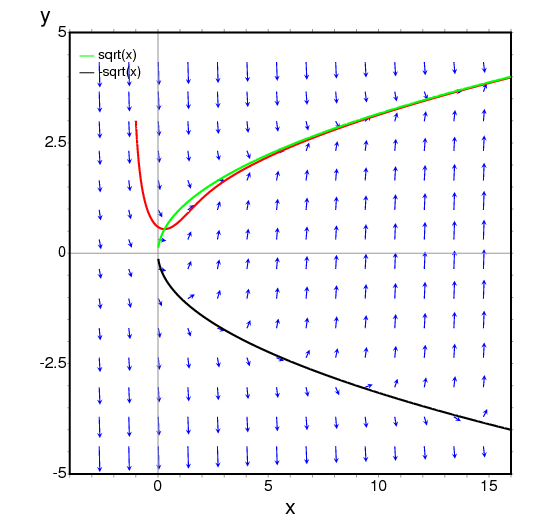
-
El siguiente ejemplo muestra el campo de direcciones de un oscilador
armónico, definido por las ecuaciones dx/dt = y y
dy/dt = -k*x/m, y la curva integral que pasa por
(x,y) = (6,0), con una barra de deslizamiento que
permitirá cambiar el valor de m interactivamente
(k permanece fijo a 2):
(%i4) plotdf([y,-k*x/m],[parameters,"m=2,k=2"], [sliders,"m=1:5"], [trajectory_at,6,0]);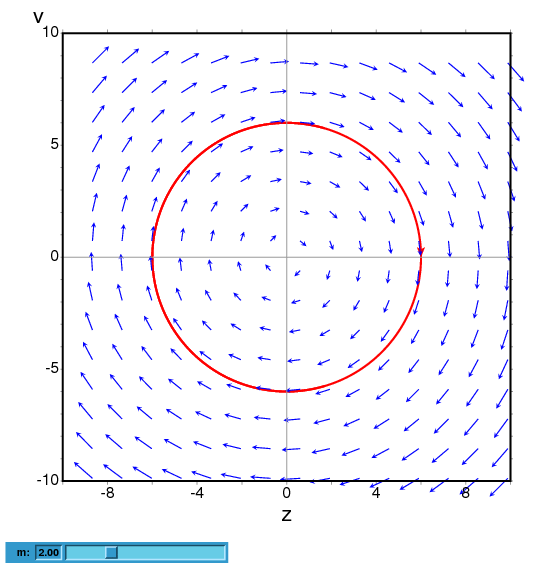
-
Para representar el campo de direcciones de la ecuación de
Duffing, m*x"+c*x'+k*x+b*x^3 = 0, se introduce la
variable y=x' y se hace:
(%i5) plotdf([y,-(k*x + c*y + b*x^3)/m], [parameters,"k=-1,m=1.0,c=0,b=1"], [sliders,"k=-2:2,m=-1:1"],[tstep,0.1]);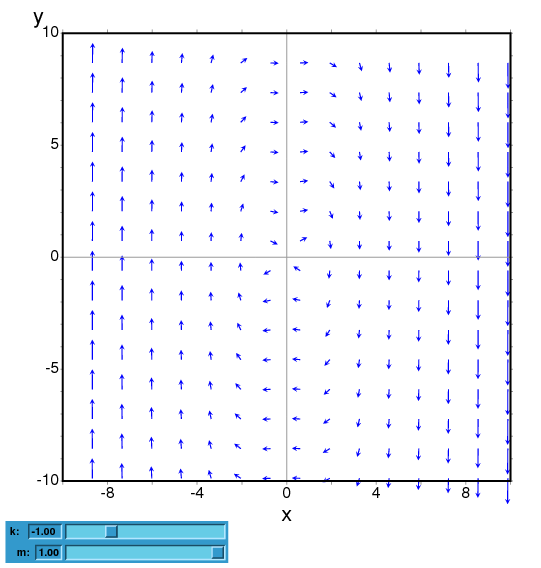
-
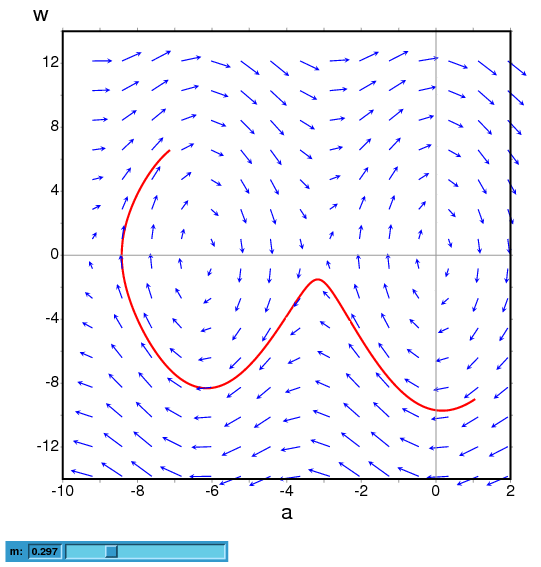
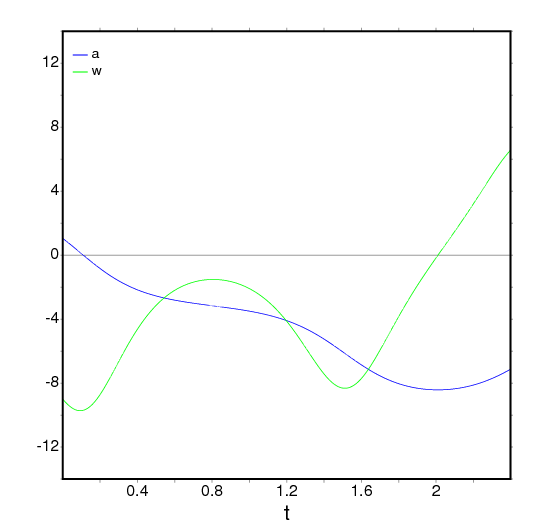
El campo de direcciones de un péndulo amortiguado,
incluyendo la solución para condiciones iniciales dadas,
con una barra de deslizamiento que se puede utilizar para
cambiar el valor de la masa, m, y con el gráfico
de las dos variables de estado como funciones del tiempo:
(%i6) plotdf([y,-g*sin(x)/l - b*y/m/l], [parameters,"g=9.8,l=0.5,m=0.3,b=0.05"], [trajectory_at,1.05,-9],[tstep,0.01], [xradius,6],[yradius,14], [xcenter,-4],[direction,forward],[nsteps,300], [sliders,"m=0.1:1"], [versus_t,1]);